UPDATE: See this blog post.
Let’s say you need a random number from 0 to 2 (0, 1, or 2). If you do this:
listing-1.c [GitHub] [Download]
your code is broken, thanks to modulo bias. You will always get modulo
bias (however slight, or great, it may be) whenever RAND_MAX + 1 of
your rand() function is not evenly divisible by your modulus n.
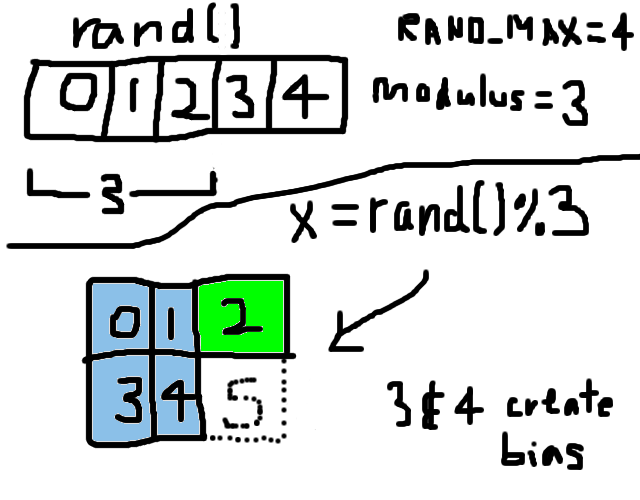
Continuing with our example, let’s say rand()’s RAND_MAX is 4, so
there are 5 different possible values that rand() can generate (0, 1,
2, 3, or 4). Now rand() will return each value 20% of the time, assuming
that rand() has very good distribution from 0 to RAND_MAX.1 But
since we take the modulo by 3, we get 0 40% of the time (0 and 3)!
This fact alone should make you worried. Visually it is as follows:
The following code is correct:
/* Listing 2 */
int n, x, rand_limit, rand_excess;
n = 3;
rand_excess = (RAND_MAX + 1) % n;
rand_limit = RAND_MAX - rand_excess;
while (x = rand() > rand_limit) {};
return x % n; listing-2.c [GitHub] [Download]
So, if RAND_MAX is 4 as in the previous example, rand_excess is \[
(4 + 1) \mbox{ mod 3}\\
= 5 \mbox{ mod 3}\\
= 2
\]. Then rand_limit becomes \(4 - 2 = 2\). The while statement then
throws out the values 3 and 4 (i.e., x is only allowed to be 0, 1, or
2). Then, we return the modulo expression x % n (which is redundant
here onlyu because RAND_MAX is very low for the sake of our example).
A problem might exist if RAND_MAX is already the maximum value allowed
by the type that rand() returns. E.g., if rand() returns a 64-bit
unsigned integer (in C99, this is the uint64_t type) , and RAND_MAX
is already set to \(2^{64} - 1\), then RAND_MAX - 1 would wrap back
around to 0, and rand_excess would likewise be 0. To avoid this, you
can use the alternate expression rand_excess = (RAND_MAX % n) + 1; for
setting rand_excess:
/* Listing 3 */
int n, x, rand_limit, rand_excess;
n = 3;
rand_excess = (RAND_MAX % n) + 1; /* only difference vs listing-2.c */
rand_limit = RAND_MAX - rand_excess;
while (x = rand() > rand_limit) {};
return x % n; listing-3.c [GitHub] [Download]
This way, you ensure that you shrink the value of RAND_MAX to
something smaller first, before adding 1 to it as in Listing 2.
Unfortunately, there still remains a problem with this workaround: there
is a remote chance that rand_excess will be equal to n, needlessly
reducing the size of rand_limit (and thus throwing away perfectly
bias-free numbers generated by rand()). For example, say RAND_MAX is
8 and n is 3. Then rand_excess is \[
(8 \mbox{ mod 3}) + 1\\
= 2 + 1\\
= 3
\]. Now rand_limit is \(8 - 3 = 5\). But RAND_MAX of 8 is already
valid because there are 9 possible values 0 through 8, and there is no
modulo bias to begin with (since \(9 \mbox{ mod 3} = 0\))! To get around
this, we can do one more modulo operation
rand_excess = ((RAND_MAX % n) + 1) % n; to avoid the case where
rand_excess could equal n:
/* Listing 4 */
int n, x, rand_limit, rand_excess;
n = 3;
rand_excess = ((RAND_MAX % n) + 1) % n; /* only difference vs listing-3.c */
rand_limit = RAND_MAX - rand_excess;
while (x = rand() > rand_limit) {};
return x % n; listing-4.c [GitHub] [Download]
So if RAND_MAX is 8 and n is 3, then rand_excess is \[
((8 \mbox{ mod 3}) + 1) \mbox{ mod 3}\\
= (2 + 1) \mbox{ mod 3}\\
= 3 \mbox{ mod 3}\\
= 0
\] and rand_limit would not be reduced by any amount.2
If you actually know beforehand the exact size of RAND_MAX (usually it
is INT_MAX or some such, determined by the type of the variable
returned by rand()), you should instead just define rand_limit as a
constant to save some CPU cycles (write out the mathematical expressions
involved by hand to find the number and just hardcode it).